Une probabilité peut en cacher une autre …

 Par ChanteClac

Vous savez quoi, c’est mon anniversaire ! Pour marquer le coup, je vais justement vous initier au célèbre problème des anniversaires : un incontournable, un tube, une source sans cesse renouvelée d’étonnement. Très bien, me direz-vous, et bon anniversaire, mais pourquoi ce titre qui annonce plutôt les maux de tête ? C’est que la curiosité du problème des anniversaires est de nature … probabiliste. Or, les probabilités élémentaires sont un magnifique cadeau pour le cerveau !

Ce qui s’énonce simplement se conçoit-il toujours bien ?

N’allons pas par quatre chemins, voici notre objet, le problème des anniversaires. Il peut s’énoncer de façon très simple : dans un groupe (par exemple le groupe des élèves d’une classe), quelle est la probabilité pour qu’au moins deux personnes aient le même anniversaire ? Je vous propose, par souci de simplicité, de nous en tenir à des années de 365 jours, reléguant ainsi le 29 février aux oubliettes. Je vous propose aussi d’ignorer le fait qu’il y a plus de naissances à certaines périodes de l’année qu’à d’autres : cette simplification revient à considérer  que chaque personne du groupe a une probabilité de 1/365 (soit 0,0027) d’être née n’importe quel jour donné de l’année.

Commencez pas faire les paris : dans un groupe de 25 personnes — effectif typique d’une classe du primaire ou du collège — quelle est, selon vous, la probabilité pour qu’il y ait au moins deux dates d’anniversaire identiques ? Voici quelques propositions :

A – cette probabilité est toute petite, inférieure à 0,1 (ce qui signifie que cela arrive typiquement dans moins de 1 classe sur 10, ou, si  vous êtes plus à l’aise avec les pourcentages qu’avec les probabilités, que cela a moins de 10% de chances d’arriver dans une classe donnée).

B – cette probabilité est petite de l’ordre de 0,2 (dit autrement, cela arrive dans environ 1 classe sur 5, ou encore, cela a environ 20% de chances d’arriver dans une certaine classe).

C – cette probabilité est moyenne de l’ordre de 0,5 (dit autrement, cela arrive typiquement dans 1 classe sur 2, ou cela a environ 50% de chances d’arriver dans une classe donnée).

D – cette probabilité est élevée, de l’ordre de 0,9 (cela arrive dans 9 classes sur 10 environ, cela a 90% de chances d’arriver dans une certaine classe).

Vous avez fait votre choix ?

Entre A et B, je suppose ? Vous vous êtes dit à la louche : « Il y a 365 dates possibles et seulement 25 personnes dans le groupe, cela fera plein de dates inutilisées, et bien peu de chances que plusieurs anniversaires tombent un même jour … ». Ou alors vous avez tenté un calcul ?

Bien sûr, la réponse n’est pas intuitive.

La voici sous forme de tableau pour quelques tailles de groupes :
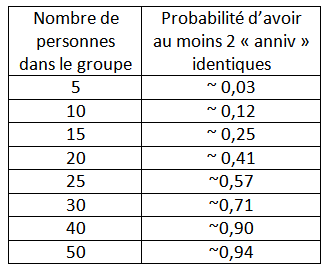Et sous forme graphique pour toutes les tailles de groupe de 2 à 100 :

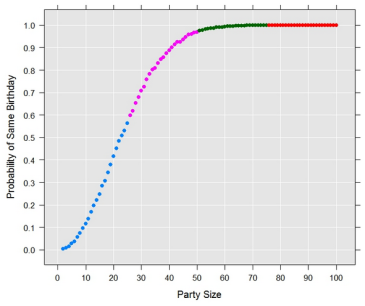Pour 25 personnes, on est à une probabilité de 0,57, soit 57% de chances d’avoir au moins deux anniversaires le même jour ! Bien étonnant, n’est-ce pas ? Je vous invite à tester la chose autour de vous, par exemple dans un établissement scolaire (celui où vous enseignez ou bien celui de vos enfants). Sur 10 ou 20 classes de 25 élèves ou plus, dans combien de classes a-t-on au moins deux dates d’anniversaire identiques ? Sans doute, dans plus de la moitié. La vidéo proposée plus bas vous suggère de refaire la « manip » en analysant les équipes des coupes du monde de football (apparemment, ces équipes sont de 23 personnes, je suppose que c’est une histoire de suppléants ? Il va falloir que j’en cause avec Elena XXL). En tout cas, riche idée pour motiver les footeux et footeuses à « expérimenter les maths« !

Equipe de France 2014

Que nous disent les probabilités élémentaires ?

Mais d’où sort ce résultat, et comment peut-on le comprendre, et cesser d’en être étonné ?

Raisonnons d’abord avec un groupe de 2 personnes, disons la personne A et la personne B. Quelle que soit la date anniversaire de la personne A, la personne B aura la même date anniversaire que la personne A avec probabilité 1/365, soit environ 0,003.

Raisonnons maintenant avec un groupe de 3 personnes, A, B et C. Pour que deux d’entre elles au moins aient la même date anniversaire, il faut : soit (AB) C, soit A (BC), soit (AC) B, soit (ABC) [par convention, j’ai choisi de mettre ensemble entre parenthèse les individus ayant la même date d’anniversaire]. Ces événements sont exclusif, et leurs probabilités se calculent ainsi :

Probabilité de (AB) C : 1 (proba que A ait une date d’anniversaire) x 1/365 (proba que B ait la même date que A) x 364/365 (proba que C ait une autre date d’anniversaire).

Probabilité de A (BC) : 1 x 364/365 x 1/365

Probabilité de (AC) B : 1 x 364/365 x 1/365

Probabilité de (ABC) : 1 x 1/365 x 1/365

On a donc au final une probabilité d’avoir au moins deux dates d’anniversaires identiques qui est la somme de ces 4 probabilités :

(3 x 364 + 1)/(365 x 365) = 0,0082 environ.

Vous entrevoyez certainement que pour traiter le cas à 25 personnes, s’y prendre ainsi va être galère ! Il va falloir sommer les probabilités de toute une série de cas, par exemple le cas (ABC) D (EF) G H I J K L M N O P Q R S T U V W X Y, le cas A B C D E F G H I J K L M N O P Q R (SY) T U V W X, le cas (A B C D E F G H I J K L M N O P Q R S T U V W) X Y, etc, etc, etc, etc, etc, etc. Rendez-vous à la Saint Glinglin … Mais en fait, il n’y a qu’un seul cas dans lequel on n’a pas au moins deux dates anniversaires identiques, le cas A B C D E F G H I J K L M N O P Q R S T U V W X Y Z. Et sa probabilité est facile à calculer : pour l’individu A, toute date convient (365/365), pour l’individu B, seules 364/365 dates conviennent, pour l’individu C, seules 363/365 dates conviennent, etc … ce qui correspond pour 25 individus à une probabilité de (365 x 364 x 363 x 362 x 361, etc … x 341) / (365^25) ou ~0,43. Ce que nous recherchons est la probabilité complémentaire à 1 (tout sauf ce cas où tout le monde a une date de naissance différente) : 1 – 0,43 = 0,57.

Appliquez cette tactique de la probabilité complémentaire au cas à 3 individus … probabilité de A B C = 365 x 364 x 363 / (365^3) = 0,9918 environ, qui est bien le complémentaire à 1 de la probabilité calculée plus haut (0,0082) avec la méthode pas maline.

Et sans calcul, ça donne quoi ?

Que vous soyez ou non convaincu par le calcul précédent, essayons de sentir la chose. Voici d’abord une petite simulation, programmée en Scratch. La simulation revient à faire entrer des personnes dans une salle initialement vide, une par une. On leur demande leur anniversaire, et on s’arrête quand la personne qui vient d’entrer annonce une date anniversaire déjà représentée par quelqu’un dans la salle.

Lancez la simulation une fois pour commencer. Regardez bien ce qui se passe. A quel effectif la simulation s’arrête-t-elle ? Lancez la simulation encore une fois. Même question. Lancez la simulation un grand nombre de fois (par exemple, 1000 fois ;-), ce qui peut se régler dans le corps du programme). Le programme garde mémoire des effectifs d’arrêt, et vous affiche le bilan à l’issue des 1000 simulations. Regardez le tableau obtenu … Comment se distribuent les effectifs d’arrêt ? Quel rapport avec les probabilités données précédemment ?

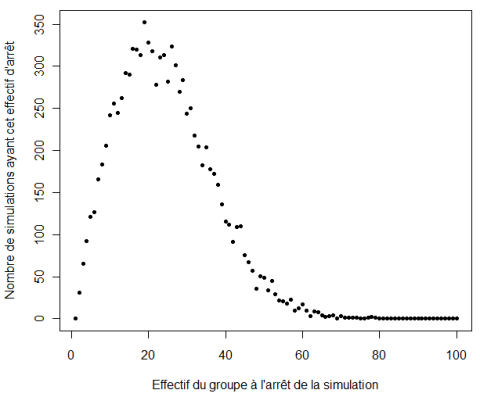
De mon côté, j’ai effectué 10 000 simulations, et représenté graphiquement la distribution des effectifs d’arrêt. Voilà ce que cela donne (L’impatience est un vilain défaut ! J’aurais eu moins de bosses dans ma distribution avec 100 000 ou 1 000 000 simulations ! ) :

La probabilité pour qu’un groupe de N personnes comporte au moins deux personnes avec leur anniversaire commun peut être estimée par la fraction des simulations de ce type qui s’arrêtent à un effectif inférieur ou égal à N. Sur mes 10 000 simulations, 309 s’arrêtent avant 5 personnes (inclus), 1233 s’arrêtent avant 10 personnes, 2578 s’arrêtent avant 15 personnes, 4212 avant 20 personnes, 5714 avant 25 personnes, 7137 avant 30 personnes, 8957 avant 40 personnes et 9715 avant 50 personnes. Divisez ces valeurs par le nombre de simulations (10 000) et vous retrouverez à un pouillème près le tableau des probabilités obtenues par la calcul.

Notre approche par simulation est donc en accord avec notre approche calculatoire, et vous a peut-être aidés à mieux visualiser les choses ?

Encore un coup de pouce pour mieux comprendre : la clé est que dans un groupe, il y a bien plus de paires d’individus que d’individus. Or, c’est le nombre de ces paires qui compte pour déterminer les chances que deux anniversaires soient identiques.

Une petite vidéo pour résumer tout ça :

Qu’avons-nous appris ?

Certains événements (dans notre cas, avoir plusieurs fois le même anniversaire dans une classe), qui paraissent très peu probables quand on y réfléchit seulement un instant,  s’avèrent être très probables. Attention, donc à l’intuition !

Une question facile à la rescousse !

Pour preuve supplémentaire que notre intuition nous trompe, posons les deux questions suivantes à deux lots de personnes (un lot répond à la première question, l’autre lot répond à la seconde question) :

Question 1 – Combien de personnes faut-il réunir dans une salle pour avoir de l’ordre d’une chance sur deux qu’au moins deux de ces personnes aient le même anniversaire ?

Question 2 – Combien de personnes faut-il réunir dans une salle pour avoir de l’ordre d’une chance sur deux qu’au moins une de ces personnes soit née le 14 juillet ?

Ce n’est pas du tout la même question ! Et pourtant dans les deux cas, la réponse la plus fréquente est « 182 » ou « 183 » personnes. Nous sommes attirés par cette réponse, sans doute parce qu’il est question d’une chance sur deux dans les deux questions. Avec moitié moins de personnes dans la salle qu’il n’y a de jours dans l’année, on se dit dans les deux cas qu’on doit être bon 😉 Pourtant, la réponse correcte à la question 1 est « 23 personnes » (voir le graphique plus haut), alors que la réponse correcte à la question 2 est « 253 personnes », ce qui est fort différent !!!!

Des questions faciles 😉

En répondant 182 ou 183, nous répondons en fait à la question triviale « Combien de jours y-a-t’il dans une demi année ? », au lieu de répondre à la question qui nous est posée. Nous donnons une réponse quasi immédiate à une question facile, et mettons la question complexe sous le tapis. C’est humain.

Avec tout cela, je suis prête pour souffler mes bougies, en essayant, comme vous, de rester curieuse.

Pour en savoir plus :

https://sciencetonnante.wordpress.com/2012/05/28/le-paradoxe-des-anniversaires/